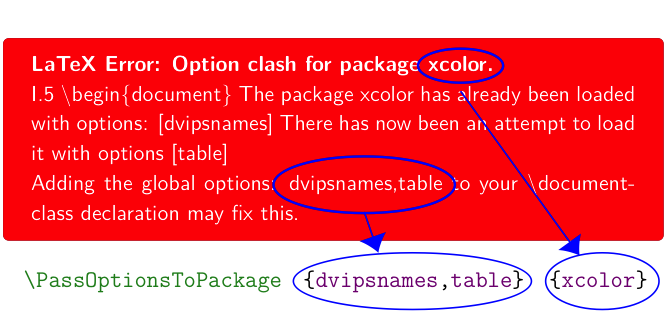
I present an easy, mechanical, highly reliable way to fix a LaTeX option-clash error that doesn’t require you to know any details about what packages you’re loading, what order you’re loading them in, or what other packages those packages load. I show you how to take two pieces of information from the error message and turn it into a \PassOptionsToPackage command to put at the beginning of your document.
Author: Jim Ratliff
Tests the Geo IP Location Wordpress plugin, returning your time zone, continent, lat/long, country, state (or other most-specific subdivision when out of the US), and city, based on your IP address.
Here are 14 chapters of lecture notes from a one-semester game-theory course I taught to students in their second year of the economics PhD program at the University of Arizona during the 1992-1997 period. The material would also be helpful to first-year PhD students learning game theory as part of their microeconomic-theory sequence, as well as to advanced undergraduates learning game theory. I consider the exposition detailed, rigorous, and self-contained.
I no longer teach game theory, so these notes are currently frozen in this state. I’m making them available here because I still get requests for them. I have not updated them to reflect subsequent advances.
These notes are in PDF format. You can download the entire course as a single compressed folder (holding 14 separate PDFs) or you can follow each chapter’s link below in the Course Table of Contents to read the abstract of, and/or download, that chapter.
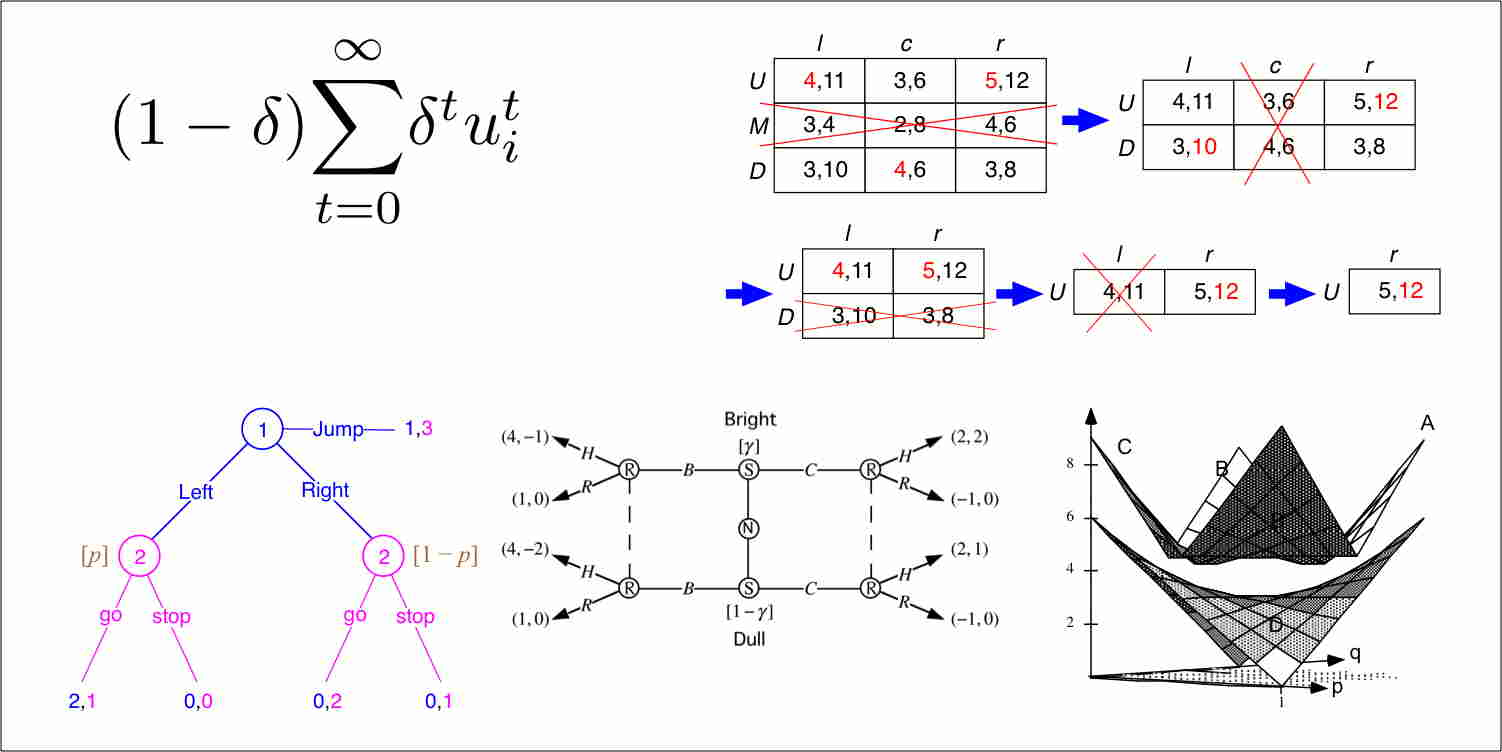
Chapter 1 of Jim Ratliff’s graduate-level game-theory course. The strategic form (or “normal form”) of a game is defined by a set of players, the actions available to each player, and each player’s payoffs to combinations of actions. We discuss best-responses to a pure-strategy profile, mixed strategies, expected payoffs to a mixed-strategy profile, the best-response correspondence, and best-response mixed strategies.
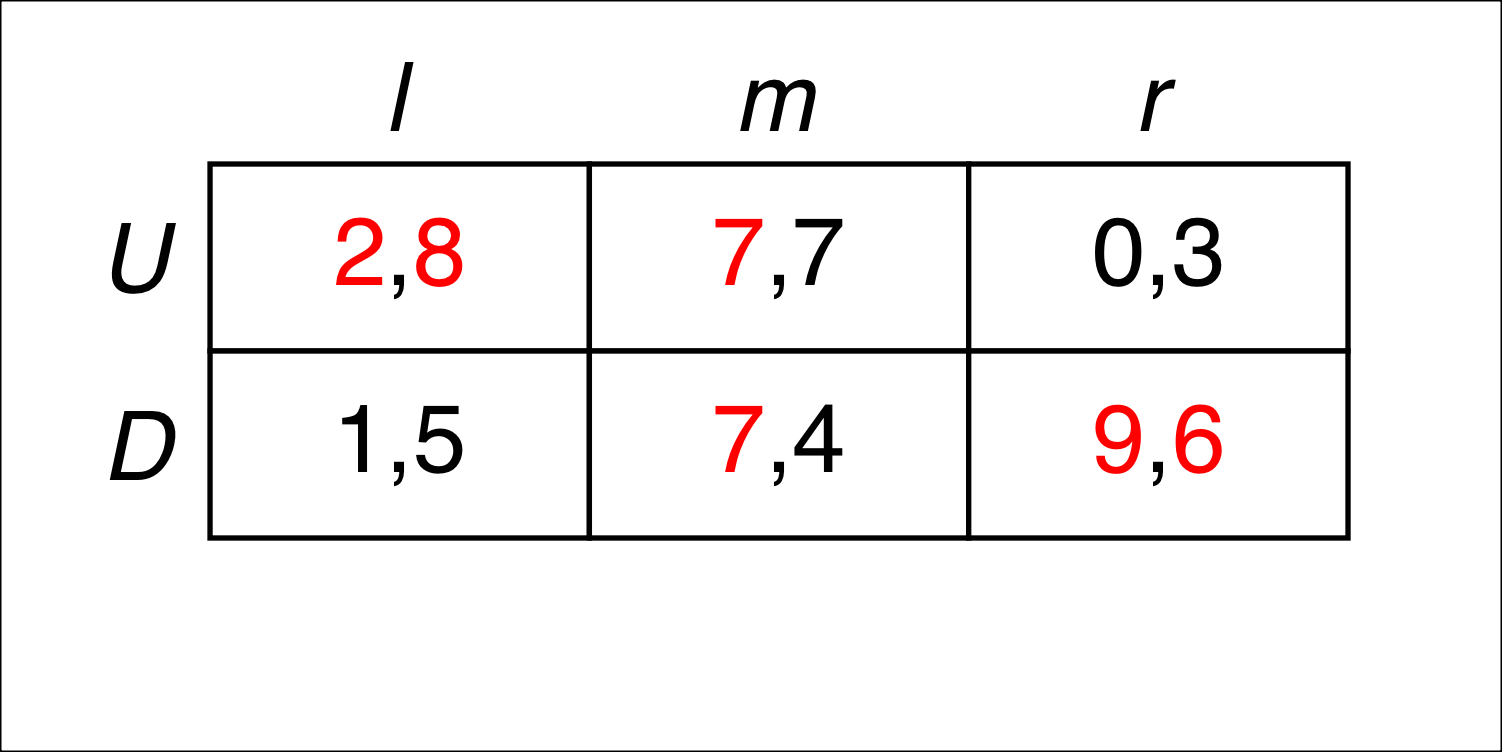
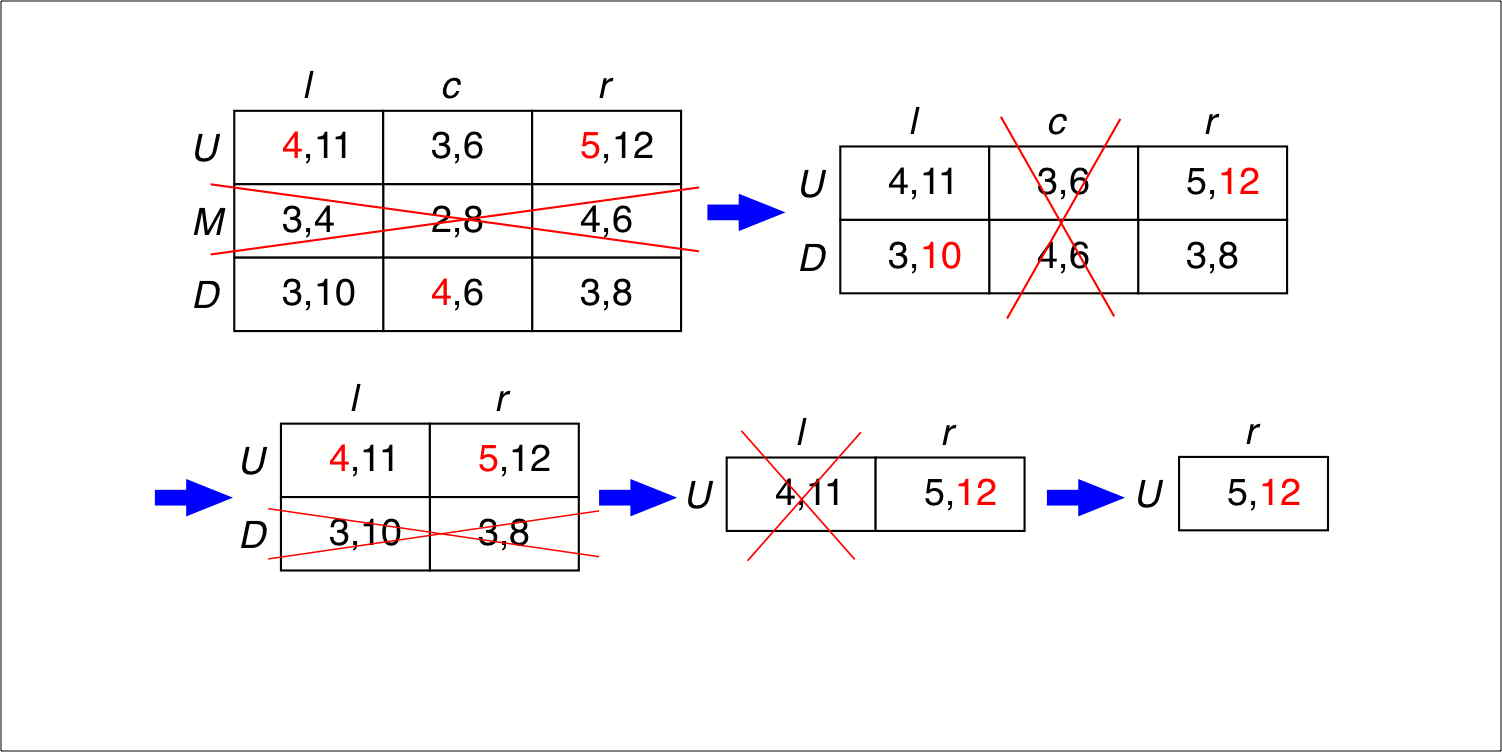
Chapter 2.1 of Jim Ratliff’s graduate-level game-theory course. Explores nonequilibrium solutions concepts based on the concept of dominance, and its close relative: never a best response. Because a rational player would never play a dominated strategy, a dominance analysis can sometimes rule out some outcomes when the game is played by rational players. Sometimes such a dominance analysis even leads to a unique prediction. In two-player games, dominance and “never a best response” are equivalent. For more than two players, never-a-best-response is stronger.
Chapter 2.2 of Jim Ratliff’s graduate-level game-theory course. Now we add the assumption: not just that the players are rational, but that they know each other is rational; and even: they each know the others know that she’s rational, etc. The infinite hierarchy of such assumptions constitutes “common knowledge.” Common knowledge justifies an iterative process of outcome rejection based on dominance or, alternatively, never a best response—which leads to the solution concept of rationalizability. Outcomes that don’t survive this process cannot plausibly be played when rationality of the players is common knowledge. Although rationality is common knowledge, some players may have had erroneous beliefs; hence some players may have ex post regret about their choice of strategy.
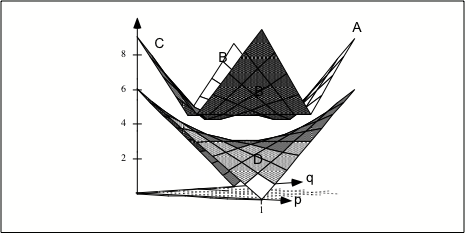
Chapter 3.1 of Jim Ratliff’s graduate-level game-theory course. When each player correctly forecasts the strategies of her opponents and then plays a best response to that forecast, the resulting strategy profile is a Nash equilibrium. Although a game need not have a pure-strategy equilibrium, John Nash proved—using Kakutani’s fixed-point theorem—that every game must have a (possibly degenerate) mixed-strategy equilibrium. Attempts to justify Nash equilibrium as either a self-enforcing agreement or the outcome of a dynamic process are problematic and deficient. Further, a Nash equilibrium can be vulnerable to multiplayer defections.
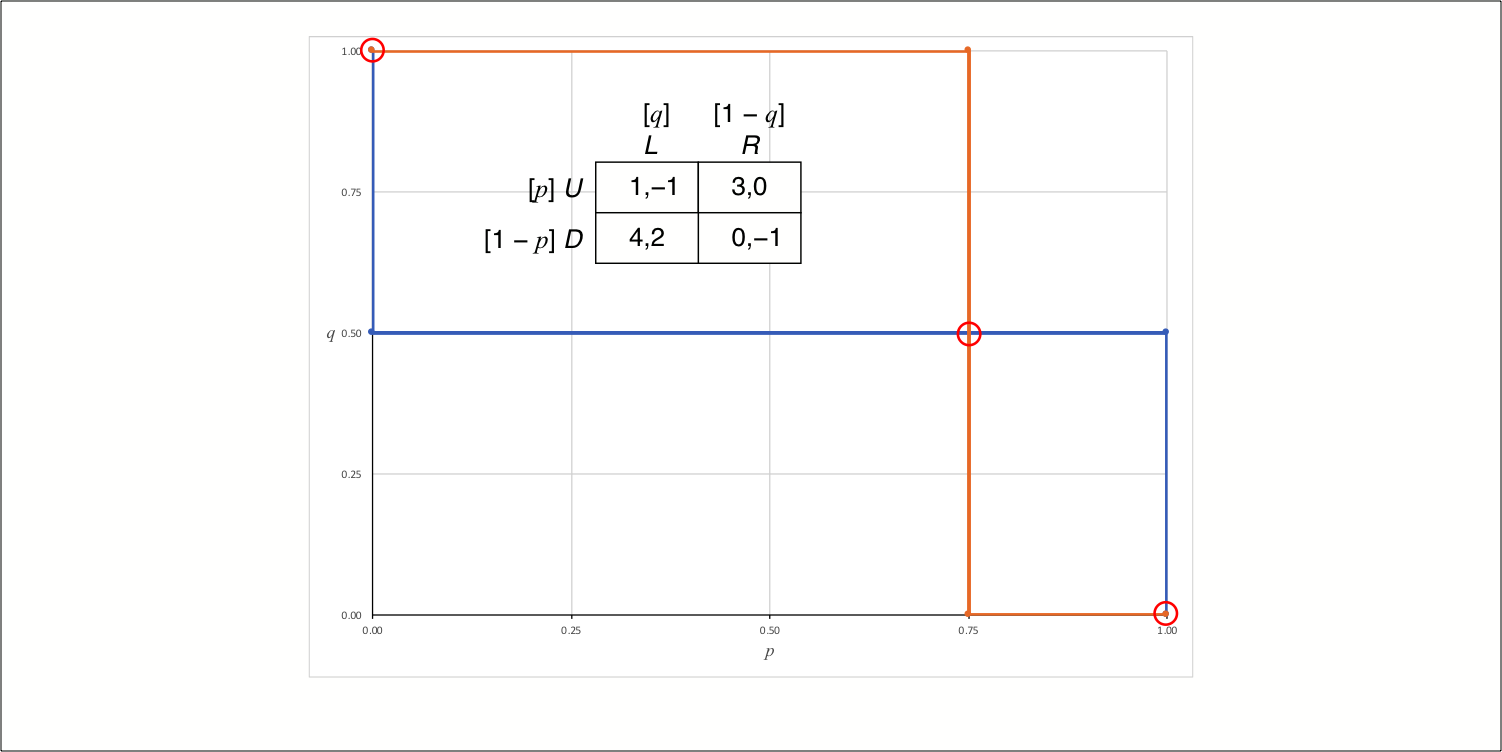
Chapter 3.1 of Jim Ratliff’s graduate-level game-theory course. We learn how to compute the set of mixed-strategy Nash equilibria for 2×2 strategic-form (“matrix”) games. For each player, we assign a mixing probability (e.g., p) to one of her strategies (and assign 1−p to the other). We determine each player’s best-response correspondence, which specifies her optimal pure strategy (or mixture over both strategies) as a function of the opponent’s mixing strategy. The Nash equilibria of the game are the points in the intersection of the players’ best-response correspondences.
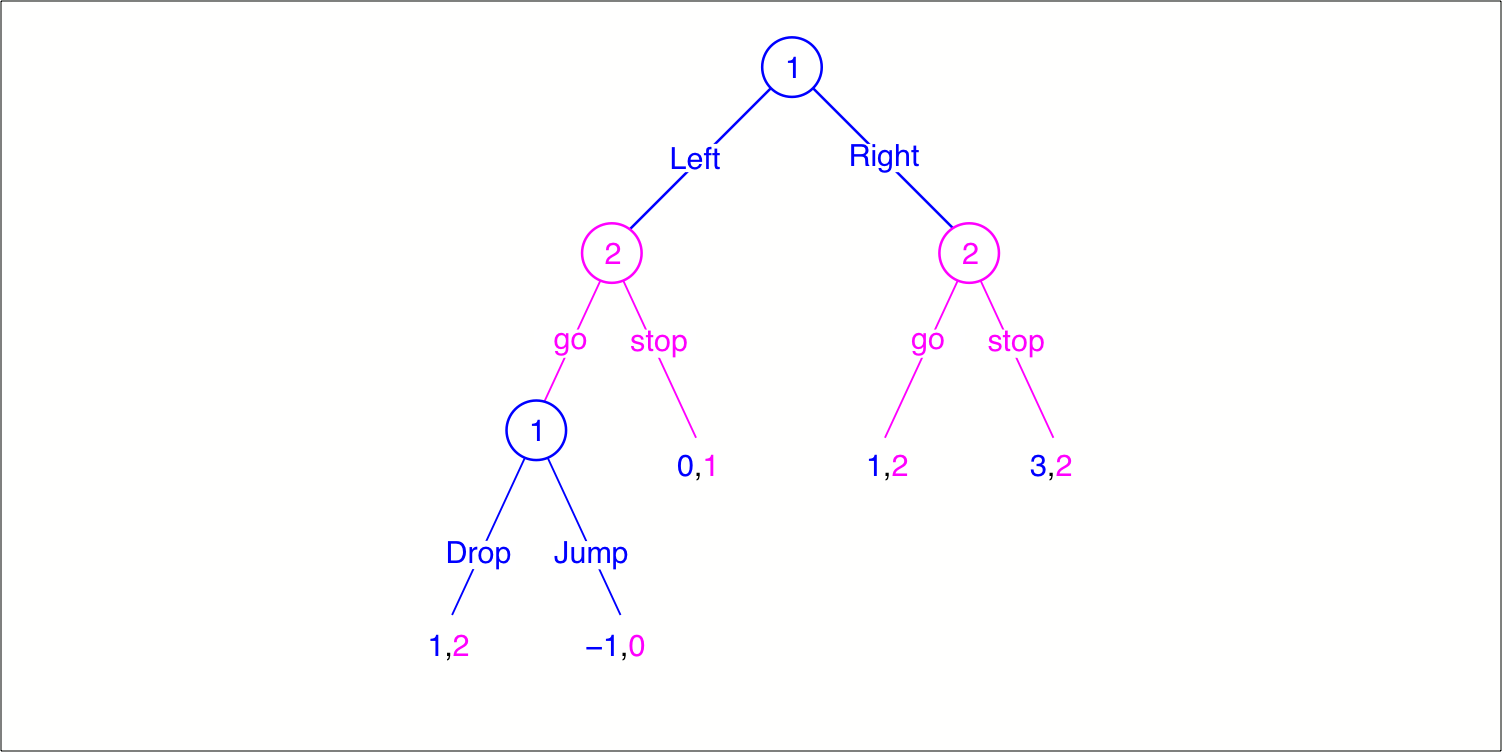
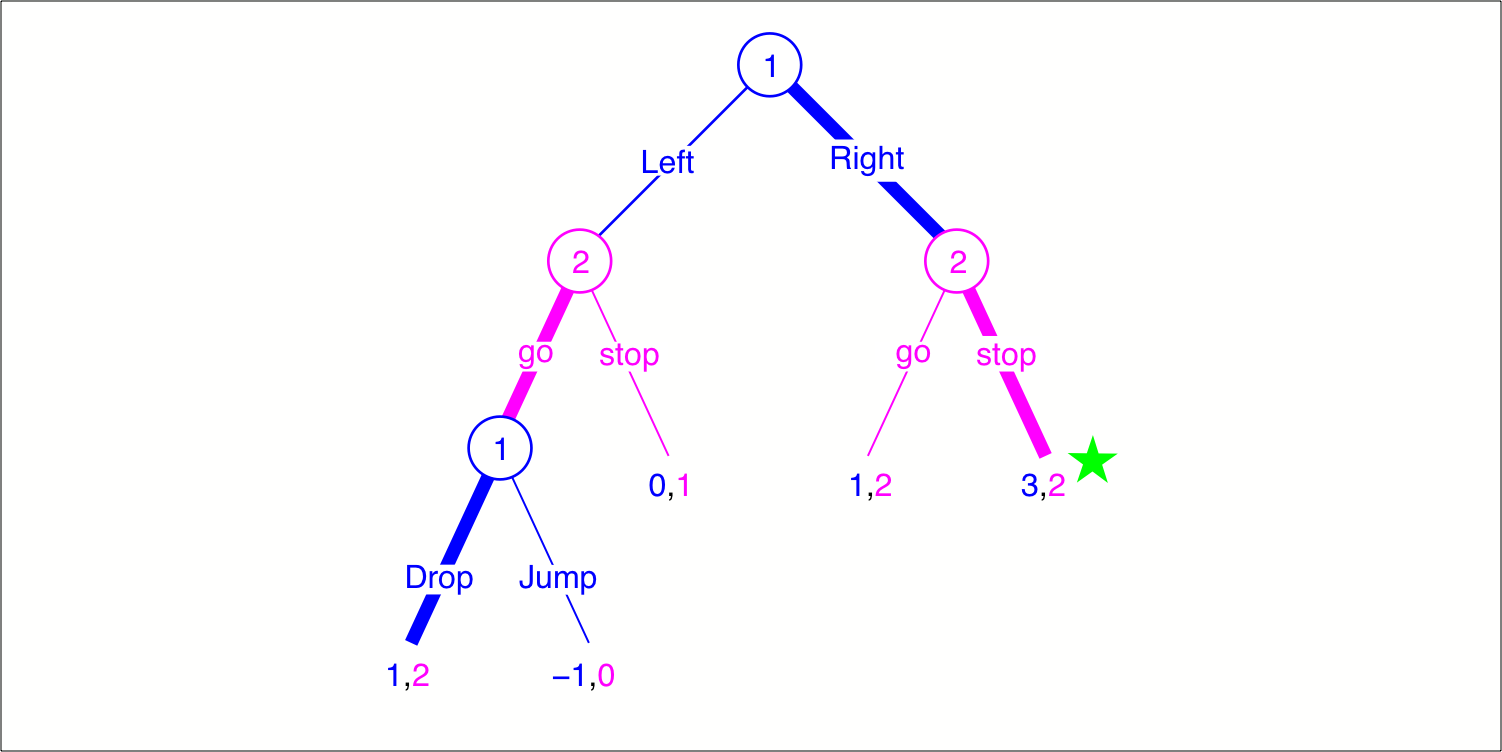
Chapter 4.1 of Jim Ratliff’s graduate-level game-theory course. The extensive form of a game can capture complex temporal and informational structure that the strategic form cannot. The extensive form elaborates upon a tree of nodes, each of which belongs to a specific player and at which that player has a defined set of actions. An information set is a set of nodes all belonging to a given player between which the player cannot distinguish when having reached one of those nodes. Collectively, the information sets define what each player knows at each point in the game. We discuss the assumption of perfect recall. We define the crucial concept of a subgame.
Chapter 4.2 of Jim Ratliff’s graduate-level game-theory course. We define a strategy for a player in an extensive-form game as a specification for each of her information sets of the (pure or mixed) action she would take at that information set. One such strategy for each player constitutes a strategy profile for the extensive-form game. Every extensive-form game can be expressed as a strategic-form game. We define how to restrict an extensive-game strategy to a particular subgame. We incorporate uncertain exogenous events into the extensive form by introducing Nature as a nonstrategic player who acts randomly. We distinguish between two different types of randomized strategies in extensive-form games: behavioral strategies and mixed strategies.