Nuance Abounds

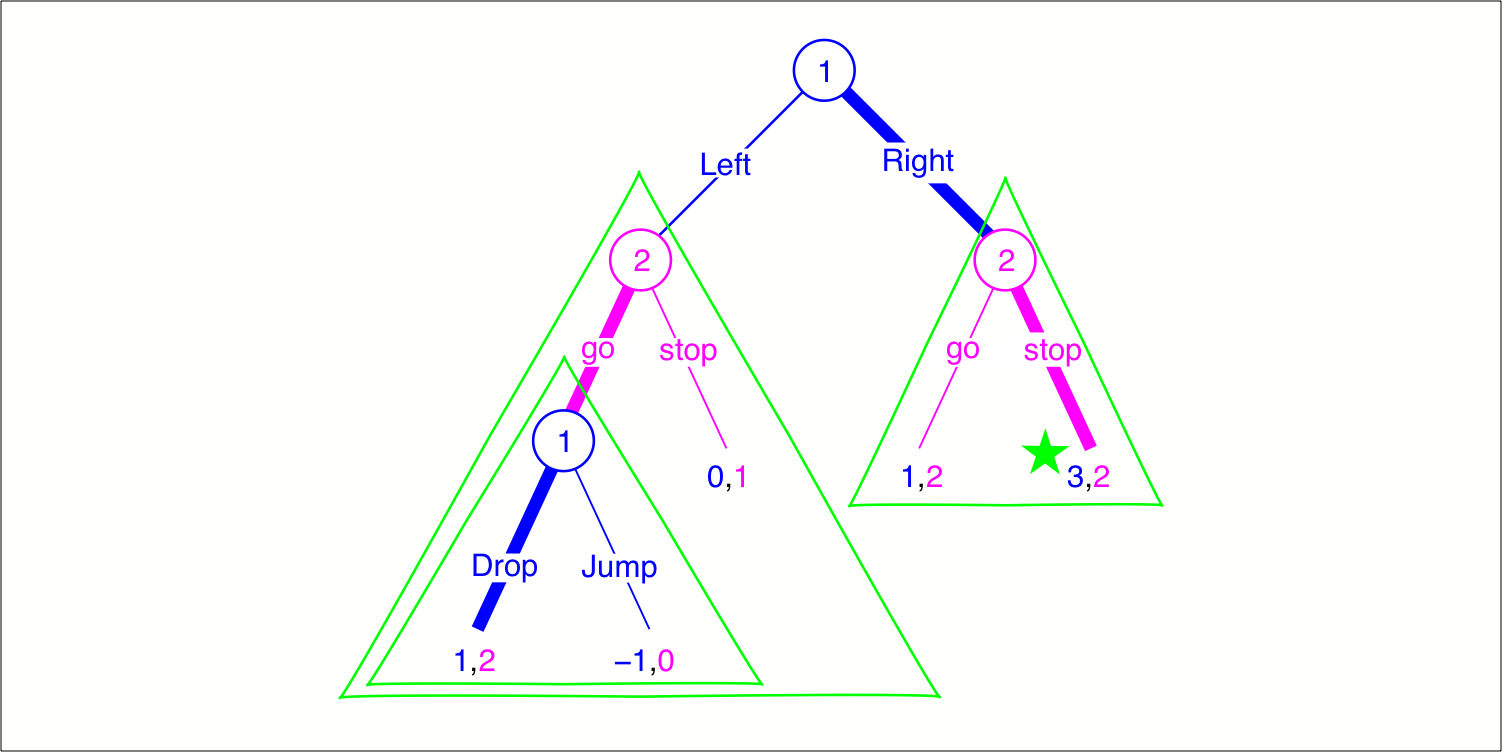
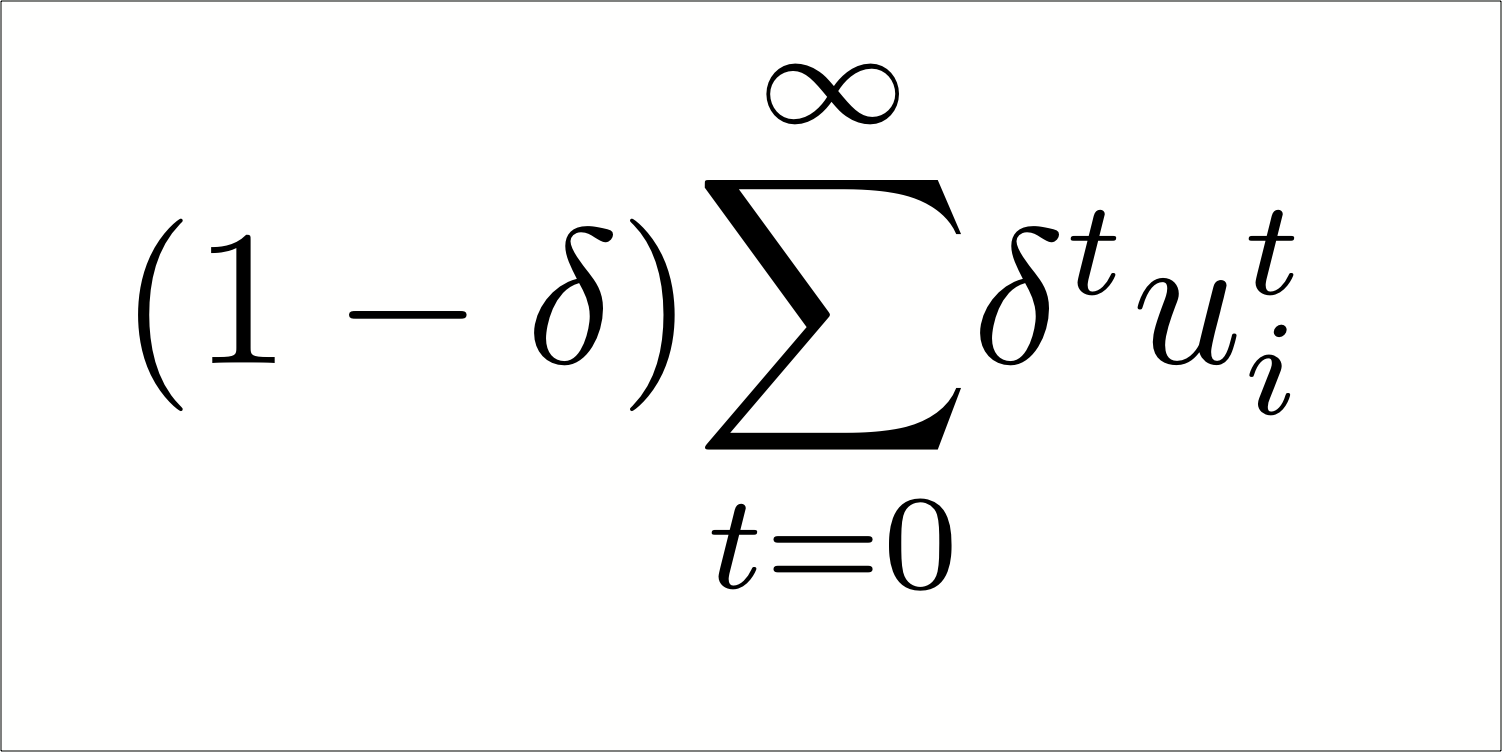Chapter 4.3 of Jim Ratliff’s graduate-level game-theory course. A rational player should also be sequentially rational: Her planned action in any situation and point in time must actually be optimal at that time and in that situation given her beliefs. We decompose an extensive-form game into a subgame and its complement, viz., its difference game. Then we learn how to restrict extensive-form game strategies to the subgame. We define the solution concept of subgame-perfect equilibrium as a refinement of Nash equilibrium that imposes the desired dynamic consistency. We use Zermelo’s backward-induction algorithm to prove that all extensive-form games of perfect information, i.e., where every information set contains exactly one decision node, have a pure-strategy subgame-perfection equilibrium. This algorithm also provides a useful technique for finding the equilibria of actual games.

Chapter 5.1 of Jim Ratliff’s graduate-level game-theory course. A repeated game is the repetition of a strategic-form “stage game,” either finitely many or infinitely many times, where the player’s payoffs to the repeated game are the sum (perhaps with discounting) of their stage-game payoffs. We define the concepts of Nash equilibrium and subgame-perfect equilibrium for repeated games. We show that any sequence of stage-game Nash equilibria is a subgame-perfect equilibrium of the repeated game. For finitely repeated games, we exploit the existence of a final period to establish a necessary condition for a repeated-game strategy profile to be a Nash equilibrium: the last period’s play must be Nash on the equilibrium path; sublime perfection requires that the last period’s play be a stage-game Nash equilibrium even off the equilibrium path. When the stage game has a unique Nash equilibrium, the subgame-perfect equilibria of the finitely repeated game are any period-by-period repetitions of that stage-game equilibrium.

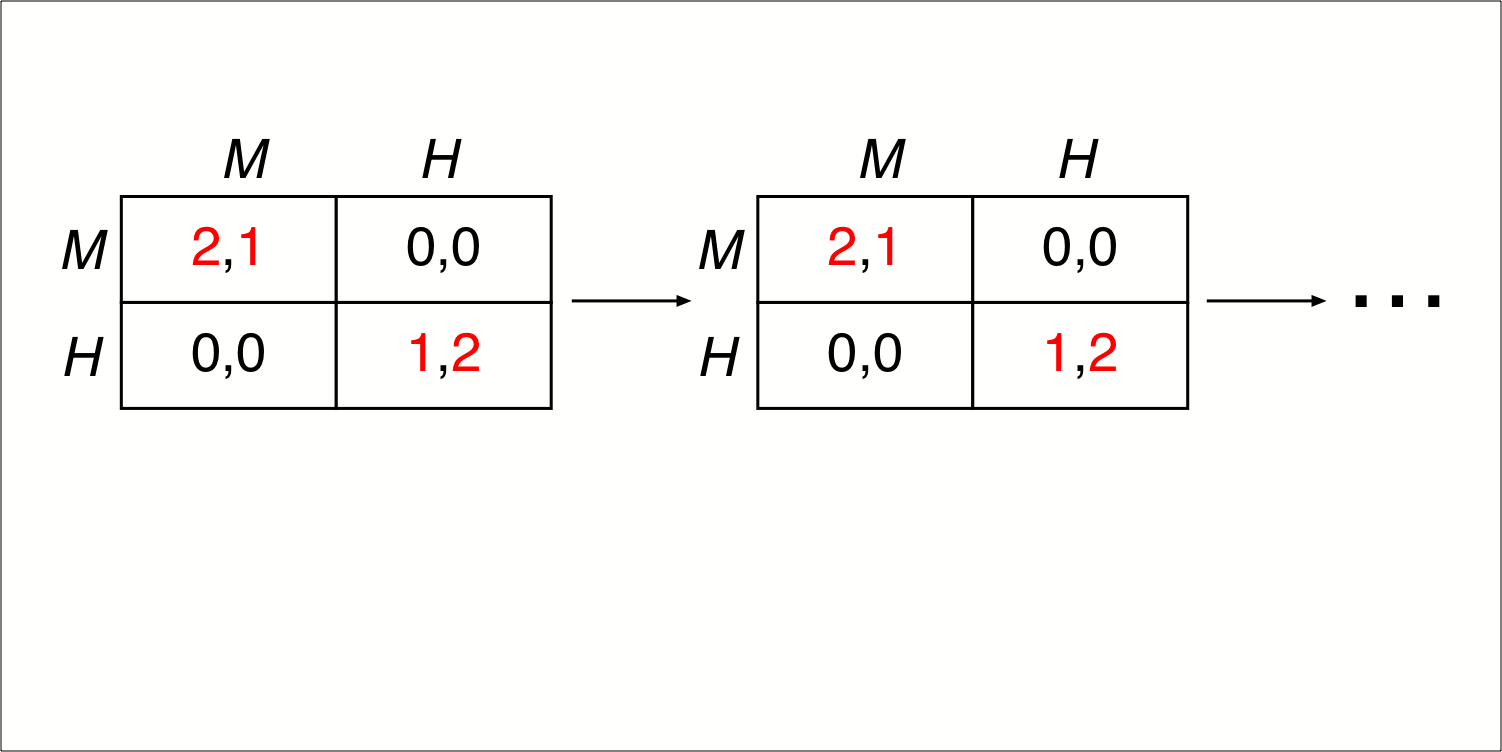
Chapter 5.2 of Jim Ratliff’s graduate-level game-theory course. When the stage game is repeated infinitely, we ensure the finiteness of the repeated-game payoffs by introducing discounting of future payoffs relative to earlier payoffs. Such discounting can be an expression of time preference and/or uncertainty about the length of the game. We introduce the average discounted payoff as a convenience which normalizes the repeated-game payoffs to be “on the same scale” as the stage-game payoffs. Infinite repetition can be key to obtaining behavior in the stage games which could not be equilibrium behavior if the game were played once or a known finite number of times. We show that cooperation is a Nash equilibrium of the infinitely repeated prisoners’ dilemma for sufficiently patient players. We show that cooperation in every period by both players is a subgame-perfect equilibrium of the infinitely repeated prisoners’ dilemma for sufficiently patient players.

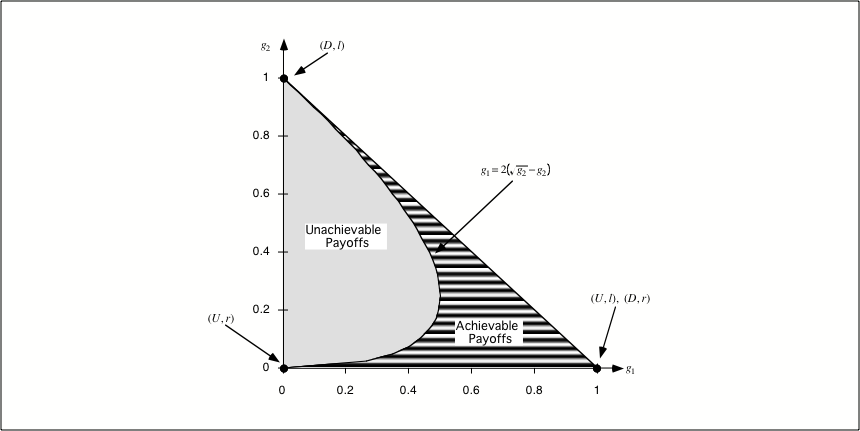
Chapter 5.3 of Jim Ratliff’s graduate-level game-theory course. A “folk theorem” in repeated-game theory is a characterization of the set of average payoffs in a class of games that are achievable in a given type of equilibrium. The strongest folk theorems are of the following loosely stated form: “Any strictly individually rational and feasible payoff vector of the stage game can be supported as a subgame-perfect equilibrium average payoff of the repeated game.” These statements often come with qualifications such as “for discount factors sufficiently close to 1” or, for finitely repeated games, “if repeated sufficiently many times.” We precisely define the terms feasible and individually rational. We state and prove two folk theorems, one Nash and one perfect, which have the virtue of being relatively easy to prove because their proofs rely only on simple “grim trigger” strategies. Then we will prove a perfect folk theorem stronger than the first two using more complicated strategies.

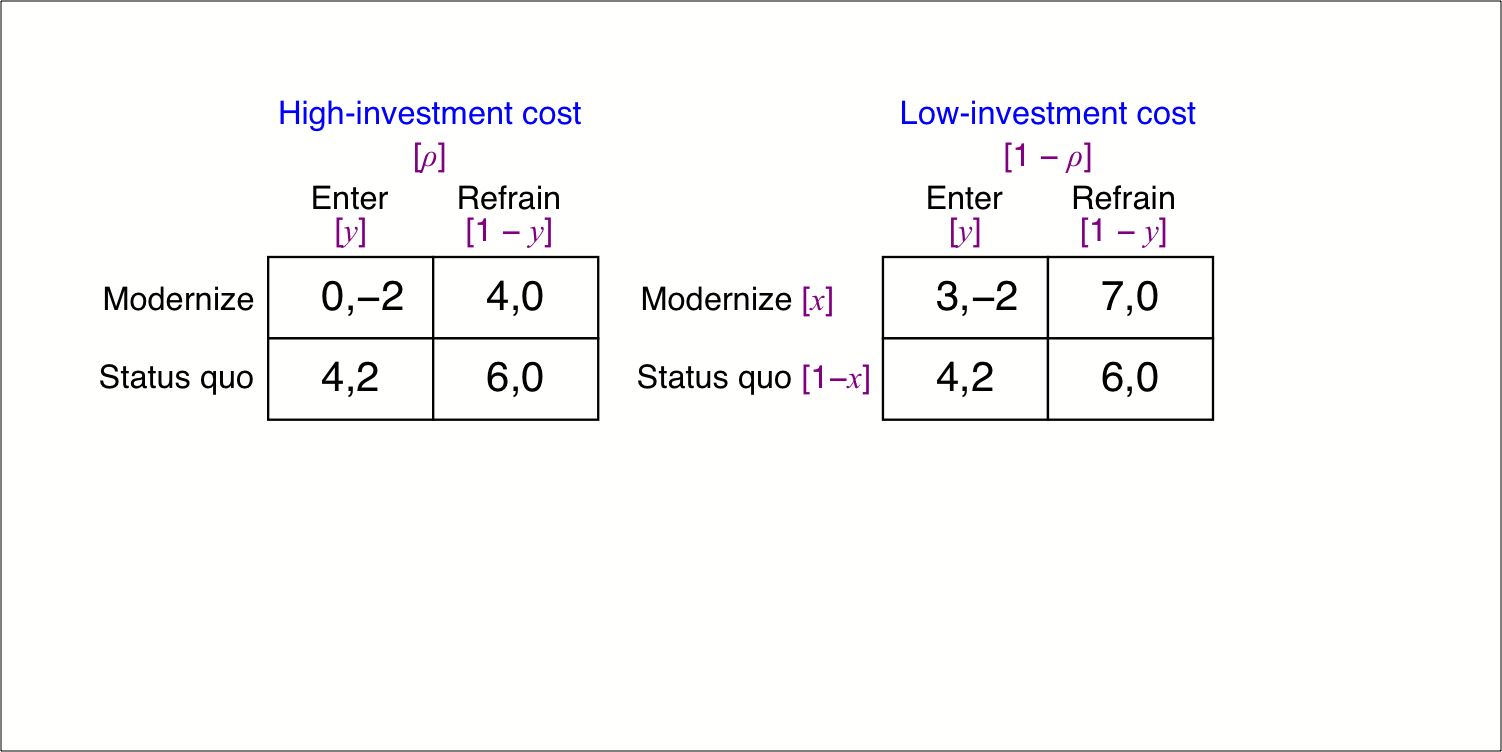
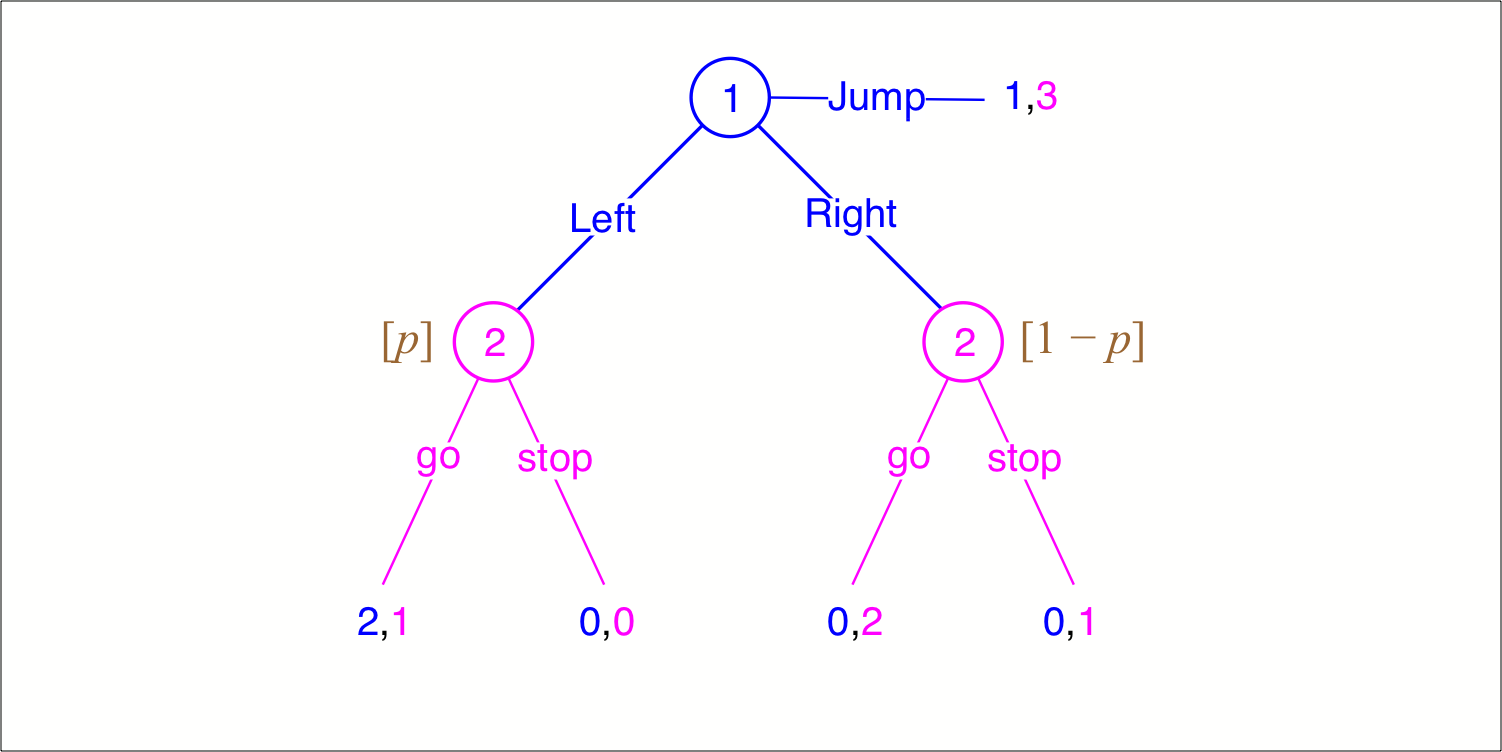
Chapter 6.1 of Jim Ratliff’s graduate-level game-theory course. A game of incomplete information, or a Bayesian game, is one where at least one player begins the game with private information, which is described by a player’s type. Each player knows her own type with complete certainty and has common-knowledge beliefs about other players’ types. A strategy for a player in the incomplete-information game is a strategy for each of that player’s types in a corresponding strategic-form game. A Bayesian equilibrium of a static game of incomplete information is a strategy profile such that every type of every player is maximizing her expected utility given the type-contingent strategies of her opponents and the probability distribution over types of each player. We consider an example from industrial-organization.

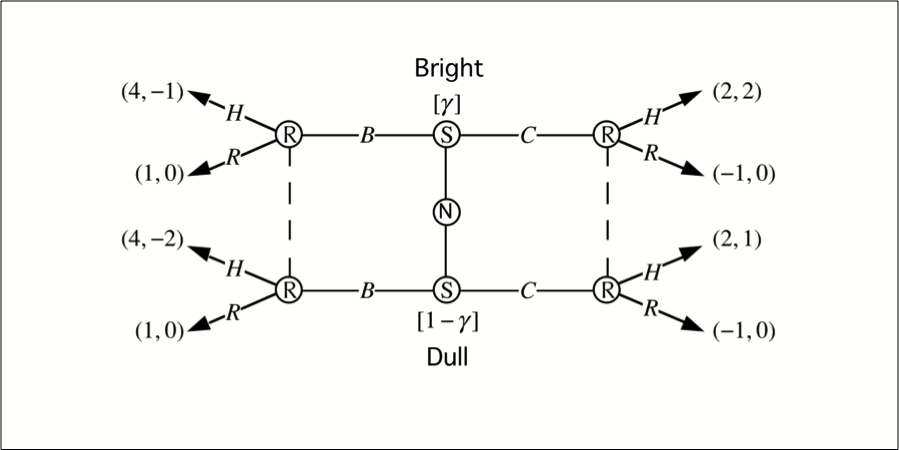
Chapter 6.2 of Jim Ratliff’s graduate-level game-theory course. Sender-receiver games are the simplest dynamic games of incomplete information. There are only two players, Sender and Receiver. Sender chooses a message m from a message space M, which Receiver observes and then responds by choosing an action a from his action space A. The Sender has private information; she can have one of two types. The Receiver has no private information and has common-knowledge prior beliefs about the Sender’s type. We define what a strategy for each player is and what a strategy profile for the game is. We define conditions on a strategy profile in order that it be a perfect Bayesian equilibrium (PBE) of the game. We consider two refinements of PBE: the Test of Dominated Messages and the Intuitive Criterion.

Even subgame perfection permits undesirable equilibria of extensive-form games. Perfect Bayesian equilibrium is a refinement of subgame perfection defined by four Bayes Requirements. These requirements can eliminate bad subgame-perfect equilibria by requiring players to have beliefs, at each information set, about which node of the information set she has reached, conditional on being informed she is in that information set.